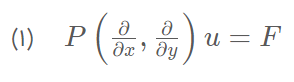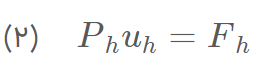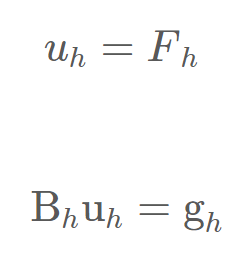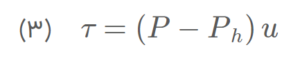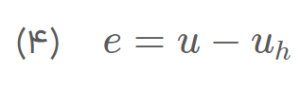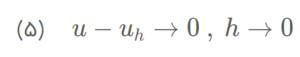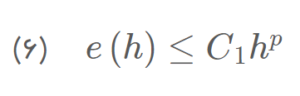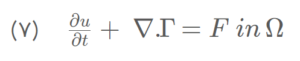بررسی روش های اجزای محدود و حجم محدود در شبیه سازی

• مقایسه روش اجزای محدود – المان محدود (Finite Element Method) و روش حجم محدود (Finite volume method)

همواره بحث‌هایی در میان مهندسین درگیر با جریان سیالات در مورد مناسب بودن روش اجزا محدود برای CFD وجود دارد. برخی از مهندسین  معتقد به برتری روش حجم محدود در مقایسه با روش‌ اجزا محدود، هستند. آیا دلیل علمی محکمی برای این نظر وجود دارد؟ به‌طورکلی نه، . روش‌های مختلف ممکن است برای مسائل  مختلف مناسب باشند.

روش‌های اجزا محدود به‌طور گسترده توسط جامعه علمی برای مطالعه روش‌های عددی جریان سیالات استفاده می‌شود. مقدار زیادی کار در مقالات علمی مرتبط با روش‌های اجزا محدود و کاربرد آن در CFD موجود است.

نرم‌افزارهای تجاری (فلوئنت، سی اف ایکس)  برای CFD به‌طور سنتی بر اساس روش‌های حجم محدود بناشده‌اند. این به خاطر این واقعیت است که به‌طورکلی همه این نرم‌افزارها دارای یک ریشه توسعه‌ای هستند. مقدار زیادی کار و فن‌آوری در این روش‌ها سرمایه‌گذاری شده است. . شیوه‌های مختلفی با دقت توسعه پیداکرده است به‌نحوی‌که بتواند با این روش‌ها مسائل را هم برای شبکه‌های با سازمان و هم شبکه‌های بی‌سازمان حل کند.

به‌عبارت‌دیگر هیچ پایه نظری یا عملی برای این فرضیه وجود ندارد که روش‌های حجم محدود نسبت به روش‌های اجزا محدود برای جریان سیال بهتر باشند. اولاً باید در نظر گرفت که روش‌های حجم محدود مختلف و روش‌های اجزا محدود مختلف وجود دارد و برخی از این روش‌ها باهم همپوشانی دارند. ثانیاً ، شیوه اجرای یک روش تأثیر بسیار زیادی بر کاربرد عملی یک نرم‌افزار دارد. برای مثال می‌توانیم بگوییم که نرم‌افزار  X کار بهتری نسبت به نرم‌افزار  Y برای یک خانواده خاص از مسائل انجام می‌دهد.  بااین‌حال، دلیل این بازده بهتر نرم‌افزار X به دلیل استفاده از روش FEM یا FVM نیست.

• روش‌های عددی و ریاضی

بیایید با یک مدل ریاضی عمومی شروع کنیم:

u=f شرط اولیه و Bu=g نیز شرط مرزی است.

در اینجا، P نشان‌دهنده عملگر دیفرانسیلی، u متغیر وابسته (متغیر حل)، F مولفه منبع، f تابع شرط اولیه ، B یک اپراتور و g یک تابع در مرز را توصیف می‌کند. x مختصات فضا در هر سه جهت (x، y، و z) را در این مورد نشان می‌دهد.

مدل ریاضی می‌تواند پدیده‌ای فیزیکی مانند جریان سیال را توصیف کند. در اینجا ، مدل نشان‌دهنده بقای مومنتوم و جرم در فضا و زمان باشد. خوشبختانه، مدل ریاضی ناشی از چنین قوانین بقا، همراه با مقادیر اولیه و شرایط مرزی کافی، اغلب خوش‌رفتار است. این به این معنی است که یک راه‌حل منحصربه‌فرد معمولاً برای چنین مسئله‌ای در شرایط مرزی و اولیه مشخص وجود دارد .

باوجود این حقیقت که یک راه‌حل منحصربه‌فرد و پایدار ممکن است برای این مسئله وجود داشته باشد ، پیدا کردن چنین راه‌حل تحلیلی ممکن است دشوار یا تقریباً غیرممکن باشد. یعنی، پیدا کردن یک عبارت تحلیلی برای حل با عملیاتی که به‌راحتی قابل‌محاسبه باشد، دشوار است . در عوض، ما باید یک مدل عددی فرموله کنیم، که یک مدل ریاضی را تخمین می‌زند. سپس معادلات مدل عددی را می‌توان با استفاده از روش عددی اجراشده در یک برنامه کامپیوتری حل کرد.

روش اجزا محدود و روش‌های حجم محدود، روش‌های عددی بر اساس گسسته سازی فضای معادلات  هستند. گسسته سازی زمانی نیز معمولاً با چند نوع طرح گام زمانی برای معادلات دیفرانسیل معمولی انجام می‌شود. مدل ریاضی تعریف‌شده در بالا مدل عددی زیر را می‌دهد:

که درآن شرط اولیه و مرزی به ترتیب به صورت زیر تعریف می شوند :

که در آن h نشان‌دهنده یک پارامتر گسسته سازی است؛ برای مثال، المان مش و یا اندازه سلول در المان محدود یا روش حجم محدود. چندین منبع خطا وجود دارد. خطای برش (truncation error) ، به ما می‌گوید که مدل عددی به چه میزان مدل ریاضی را تخمین می‌زند:

مرتبه  دقت (order of accuracy) مدل عددی به ما نشان می‌دهد که با چه سرعتی خطای برش (برش) با کاهش h کاهش می‌یابد. این به این معنی است که هر چه المان‌ها کوچک‌تر شوند یا اندازه سلول کوچک‌تر باشد، تفاوت بین مدل ریاضی و عددی باید کمتر شود. چنانچه خطای برش به همراه کاهش h کاهش داشته باشد، یک مدل عددی پایدار است.

خطای گسسته سازی (discretization error) در ‌حل به‌عنوان تفاوت بین راه‌حل دقیق و راه‌حل عددی برای معادلات  تعریف می‌شود:

حل عددی زمانی همگرا  (converge) می‌شود که در آن مقدار جواب حل عددی به حل دقیق نزدیک شود که با کاهش h رخ می‌دهد:

مرتبه دقت گسسته سازی، به ما نشان می‌دهد که راه‌حل عددی با چه سرعتی به راه‌حل دقیق با کاهش h همگرا می‌شود:

هرچه p بزرگ‌تر باشد تقریب با سرعت بیشتری همگرا می‌شود.

بنابراین آیا تفاوت ذاتی در دقت روش‌های اجزا محدود و روش‌های حجم محدود وجود دارد؟ با افزایش مرتبه  توابع پایه، می‌توان ازلحاظ نظری به هر درجه دقت با روش‌های اجزا محدود (در عمل، محدودیت‌های دیگری نیز وجود دارد) رسید. رایج‌ترین روش‌های المان محدود به ترتیب مرتبه دوم تا  مرتبه سوم هستند، و روش‌های حجم محدود مرتبه اول تا مرتبه دوم هستند.

• تفاوت‌ها و شباهت‌های روش‌های المان محدود و حجم محدود چیست؟

بیایید نگاهی به معادله موازنه شار بیندازیم که اساس مدل‌های ریاضی برای جریان سیال را تشکیل می‌دهد:

در این معادله، u مقدار فیزیکی در بقا از قبیل تکانه یا جرم را مشخص می‌کند و Γ بیانگر شار این مقدار است؛ برای مثال، شار مومنتوم در هر واحد سطح کنترل و در واحد زمان .

روش‌های اجزا محدود با فرموله کردن یک معادله انتگرالی شروع می‌شود‌ که در آن معادلات با تابع آزمون ϕ نوشته می‌شوند و میانگین‌گیری با انتگرال‌گیری در دامنه مدل انجام می‌شود:

اگر قضیه دیورژانس را بر روی Γϕ اعمال کنیم :

در اینجا، ƏΩ نشان‌دهنده مرز دامنه است و n نشان‌دهنده بردار نرمال به مرز دامنه است. انتگرال‌گیری از سمت چپ در معادله بالا نتیجه زیر را می‌دهد:

در اجرای عددی، درنهایت این مسئله منجر به این مزیت می‌شود که بردار شار نیاز به قابل دیفرانسیل‌گیری بودن نداشته باشد که منجر به معادلات مورداستفاده به‌عنوان نقطه شروع در روش‌های اجزا محدود می‌شود:

این حالت از معادله انتگرالی را به‌اصطلاح فرم ضعیف معادلات می‌گویند.  فرم ضعیف معادلات تنها زمانی می‌تواند حالت فیزیکی مدل را نشان دهد که تغییرات وسیع تابع آزمون را در نظر گیرد.  یک حالت رایج مورداستفاده برای تابع آزمون توابع چند جمله ای هستند. اما زمانی که تابع آزمون را برابر یک (مقدار ثابت) قرار دهیم به حالت زیر از معادله 11 می‌رسیم که معمولاً به‌عنوان نقطه شروع روش حجم محدود در نظر گرفته می‌شود:

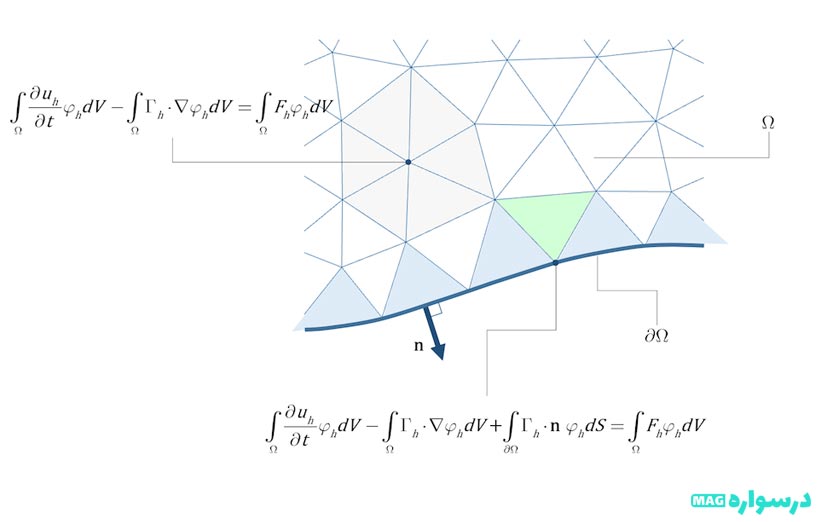
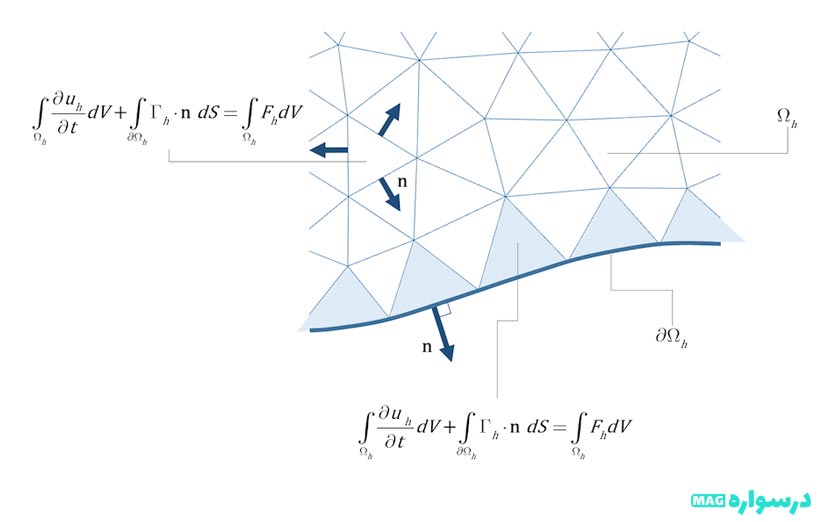
تاکنون، تفاوتی بین اجزا محدود و روش‌های حجم محدود وجود ندارد. همان‌طور که در بالا می‌بینیم، معادله روش حجم محدود،  فقط یک حالت خاص از فرم ضعیف عمومی است که در روش‌های اجزا محدود استفاده می‌شود. تفاوتی که وجود دارد در شیوه گسسته سازی معادلات مورداستفاده در هر مورد است. روش المان محدود با انتخاب تعداد محدودی تابع آزمون  و حل فرم ضعیف معادلات به دست می‌آید و روش حجم محدود با انتخاب تعداد محدودی از حجم محدود ها (Control Volume) و حل معادله 12 به دست می‌آید. به‌این‌ترتیب شکل‌های 1 و 2 فرم گسسته سازی شده معادلات را به ترتیب برای روش المان محدود و روش حجم محدود با استفاده از شبکه مثلثی را نشان می‌دهند.

شکل (1)

اگر به رایج‌ترین روش‌های اجزا محدود نگاه کنیم، آنگاه می‌بینیم که توابع آزمون تنها در مجاورت گره‌ها (تابع پشتیبانی محلی) غیر صفر هستند. این به این معنی است که انتگرال فقط باید بر روی عناصر (در اینجا، مثلث) و حوالی آن محاسبه شود.

در عوض اگر به روش‌های معمول حجم محدود  نگاه کنیم، هر سلول (مثلث) به‌عنوان یک دامنه منفرد رفتار می‌شود.

در روش‌های اجزا محدود، اغلب توابع پایه مشابه برای تخمین راه‌حل به‌عنوان توابع آزمون به کار می‌روند. تا زمانی که تخمین راه‌حل دارای درجه چندجمله‌ای بالاتر از صفر باشد و مشتقات درجه اول را بتوان تقریب زد، هیچ نیازی نیست که هیچ کار خاصی  برای حل یک شار همرفتی و دی فیوز انجام داد. بردار شار نیز یک تابع چندجمله‌ای محلی است.

از طرف دیگر، در حجم محدود، حل در مرز به‌خوبی تعریف‌نشده است. این روش تنها مقدار ‌حل را برای هر سلول  در مرکز سلول تعریف می‌کند. بنابراین روش حجم محدود حتماً باید با یک روش بازسازی تعریف شود. به‌طورمعمول، یک روش درون‌یابی محلی برای در نظر گرفتن مقادیر در سلول‌های مجاور تعریف می‌شود.

بسته به توابع پایه مورداستفاده درروش اجزای محدود و نوع ساختار تعریف شارها در روش حجم محدود، دقت های مختلف را می‌توان به دست آورد. یک شبکه درشت با روش مرتبه دوم می‌تواند یک راه‌حل دقیق‌تر از یک مش بهتر با یک روش مرتبه اول به دست آورد.

شکل (2)

توابع آزمون خطی و توابع پایه برای روش اجزای محدود به‌طورمعمول به روش‌های مرتبه دوم و دقیق منجر می‌شوند. المان‌های محدود در گسسته سازی انعطاف‌پذیری زیادی دارند. برای مثال استفاده از توابع پایه درجه‌دو نسبتا ساده است. نیازی به بازسازی یا درون‌یابی حل وجود ندارد.

یک ایراد روش FEM (اجزای محدود) این است که برای توابع آزمون و پایه مداوم هیچ موازنه محلی برای مقادیر قابل‌تعریف نیست. به‌بیان‌دیگر تنها شار کلی در میدان  از قوانین موازنه پیروی می‌کند. عیب دیگر این است که هیچ کنترلی از شارهای محلی وجود ندارد که پایدارسازی گسسته سازی جریان‌های جابجایی را سخت‌تر می‌کند.

در سوی دیگر روش المان محدود این مزیت را دارد که قادر به فرموله کردن توابع پایه با مراتب مختلف است. مراتب بالاتر برای توابع پایه، امکان افزایش دقت برای شبکه‌های مختلف را فراهم می‌کند.

همان‌طور که قبلاً ذکر شد، روش‌ FVM متناظر با یک تابع پایه المان محدود تکه‌ای، احتمالاً با یک طرح درون‌یابی مرتبه بالاتر برای شارها است که منجر به‌دقت مرتبه اول یا دوم می‌شود. بیان محلی از روش حجم محدود باعث امکان تعریف موازنه و بقا به‌صورت محلی می‌شود که جنبه جذاب روش حجم محدود است.

• نتیجه‌گیری نهایی در مورد FEM Vs FVM

همان‌طور که ذکر شد شباهت‌ها ، تفاوت‌ها، برتری‌ها و معایبی بین دو روش نسبت به هم وجود دارد. جنبه‌های دیگر مهم و تأثیرگذار برای انجام یک شبیه‌سازی سیالاتی همچون حل دستگاه بزرگی از معادلات خطی سازی شده، تنظیمات مرتبط با گام‌های زمانی و تنظیمات مرتبط با گام‌های زمانی ضمنی و صریح و … نیز وجود دارد. انواع روش‌های موجود نیز درحال‌توسعه هستند که فرصت‌های جدیدی را فراهم می‌نمایند.