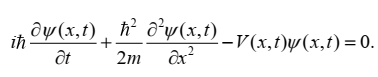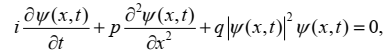یکی از معادلات مهم درمکانیک کوانتوم معادلات غیرخطی شرودینگر می باشد. بررسی سیستم های فیزیکی می تواند به شکل تک ذره ای و یا بس ذره ای انجام گیرد. پاسخ کوآنتومی این نوع از سیستم ها، معمولاً با حل یک معادلۀ شرودینگر آغاز می گردد و سرانجام، ادامه کمیات فیزیکی به همراه این پاسخ ها حاصل می گردد.همچنین، محاسبه انرژی های معادله شرودینگر در فیزیک قابل اهمیت است. به عنوان مثال در محاسبه میزان جذب نور.
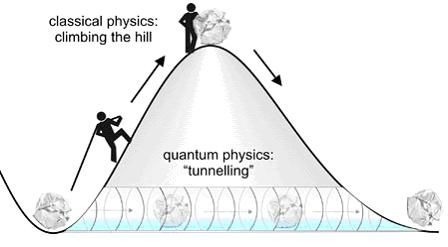
بعلاوه، معادله شرودینگر معادله اصلی و پایه ای مکانیک کوانتومی می باشد و مشابه همان نقشی را که معادله قانون دوم نیوتن به عنوان معادله پایه درمکانیک کلاسیک ایفا می کند در مکانیک کوانتومی برعهده دارد. در این جا تونل زنی کوانتومی مطرح می شود بدین معنا که، از نگاه فیزیک کلاسیک یک ذره که پشت یک سد پتانسیل گیر کرده است، انرژی و امکان لازم برای عبواز مانع را ندارد. مطابق شکل اگر این سنگ بخواهد به سمت دیگر تپه برود، ناچارا باید شخصی آن را به بالای قله برده و از آنجا به پایین هل دهد، ولی مکانیک کوانتوم راه را آسان کرده و بیان می کند: سنگ می تواند با زدن تونل از دل کوه عبورنماید .بنابراین مطابق اصل عدم قطعیت هایزنبرگ، نمی توان مکان و اندازه حرکت یک ذره را باهم اندازه گیری نمود و ما هیچگاه قادرنیستیم مکان یک ذره را با اطمینان کامل مشخص کنیم، درحالیکه، همیشه این مقدار با عدم قطعیتی همراه خواهد بود. درنتیجه، همواره برای حضور ذره در هر جایی احتمالی هست! بدین معناکه برای حضور ذره در آن سمت تپه هم احتمال معینی وجود دارد و ممکن است ذره بتواند به شکل موقت انرژی گرفته و سرانجام از مانع یا سد مقابل خود عبور کند و آن سوی آن حرکت کند. براساس معادله شرودینگر هر چه ارتفاع و عرض این مانع کمتر باشد احتمال عبور ذره ازبین آن بیشتر خواهد بود.
موضوع دیگری که در این جا مطرح می شود معادله دیراک می باشد.
در اصل، معادله دیراک، معادلهای در مکانیک کوانتومی و تعمیم یافتهٔ معادله شرودینگر برای محاسبه تابع موجی ذرّات می باشد. با این تفاوت که این معادله نظریه نسبیت خاص را در نظردارد. بعلاوه، این معادله توسط فیزیکدان بریتانیایی پل دیراک به وجود آمد که خود دیراک این معادله را بر مبنای معادله کلاین-گوردون گسترش داد. در این مسیر او نیاز به حالت های با تکانه زاویه در طبیعت را کشف نمود. همچنین، این موضوع به ویژه در تعبیر حالت های با انرژی منفی مفید می باشد. علاوه براین، معادله شرودینگر معادله ای است که چگونگی تغییر حالت کوانتومی یک سامانه فیزیکی با زمان و یا چگونگی توزیع احتمال حضور یک ذره در بازه بخصوصی از مکان راتوصیف می نماید. در حالت اول از یک معادله شرودینگر وابسته به زمان و در حالت دوم از یک معادله شرودینگر مستقل از زمان استفاده می شود.
مطلب قابل توجه این است که، در تفسیر استاندارد مکانیک کوانتومی، تابع موج کاملترین توضیحی می باشد که میتوان در مورد یک سامانه فیزیکی داد. بعلاوه، همانند قانون دوم نیوتن، معادله شرودینگر از لحاظ ریاضی می تواند به فرمولبندی های دیگر از جمله مکانیک ماتریسی ورنر هایزنبرگ و فرمولبندی انتگرال سطحی زیمان تبدیل شود. در کل، معادله شرودینگر یک معادله وابسته به زمان است که با فرض جوابی به صورت ضرب یک تابع مجهول تنها (وابسته به مکان) در یک تابع نمایی (تنها تابعی از زمان) می توان با کمک روش جداسازی متغیرها آشکار ساخت که تابع مجهول در معادله مستقل از زمان شرودینگر صدق می نماید.
لازم به توضیح هست که در اپتیک غیر خطّی، با بسط بسامد زاویه ای یک موج بر حسب عدد موج و دامنۀ آن می توان معادلۀ غیر خطّی شرودینگررا به دست آورد. بر همین اساس اگر بسامد زاویه ای موج را در حضور کمینه طول مشاهده پذیر محاسبه کنیم، با بسط بسامد زاویه ای تعمیم یافتۀ موج به معادلۀ غیر خطّی شرودینگر در حضور کمینه طول می توان دست یافت.
معادله غیر خطی شرودینگر به شکل زیر تعریف می شود:
اگر پتانسیلِ به خودِ ϕ وابسته باشد جملۀ آخر معادلۀ شرودینگر را غیر خطّی میکند و معادله به صورت معادلۀ غیرخطّی شرودینگر زیر تبدیل خواهد شد.
مسئله ی وابسته به زمان شرودینگر با تابع پتانسیل دلخواه، یکی از اساسی ترین معادالت مکانیک کوانتوم است. معادالت شرودینگر نقش اساسی در مکانیک کوانتوم نسبیتی و غیرنسبیتی دارند. برای مثال، در 9111 تورس- وگا و فردریک معادالت شرودینگر را برای نشان دادن فاز تازه ای از مکانیک کوانتوم مدلسازی کردند. بعلاوه بسیاری از مسائل علوم مهندسی از جمله اپتیک، زلزله شناسی و فیزیک پالسما منجر به ایجاد این معادله می شود.
اگر تاریخچه مختصری از اروین شرودینگر بخواهیم بگوییم، اروین شرودینگر فرزند یگانه یک خانواده قدیمی دانشدوست اتریشی است، به تاریخ 12 اوت 1887در وین چشم به جهان گشود. تا 11 سالگی درخانه درس خواند. سپس به مدرسه متوسطه رفت و درسال 1906 وارد دانشگاه وین شد.در 1910 درجه دکتری گرفت. بعدا عنوان دانشیاربه خود گرفت .همچنین دانشیار جوان در سال 1920 موفق به دریافت جایزه خود از آکادمی تحقیقات اتریش شد.درهمین سال به معاونت ماکس ویسن انتخاب گردید.
بعلاوه، در سال 1921 شرودینگربه استادی فیزیک ریاضی دانشگاه زوریخ منصوب شد.در همین زمان مکانیک موجی خویش را مطرح نمود که معادله موجی شرودینگر نامیده می شود. شهرت علمی اش موجب شد، در 1928از میان داوطلبان زیادجانشین ماکس پلانک، وی را به دانشگاه برلن دعوت کنند که تا سال 1933دراین شهر اشتغال داشت. به فرموده ماکس پلانک، این معادله پایه ای برای مکانیک کوانتومی جدید ایجاد نموده است.
بعدها شرودینگررا از زوریخ دعوت کردند تا در دانشگاه برلن جانشین ماکس پلانک شود. لازم به ذکر است که در مقایسه با فیزیک کلاسیک، معادلۀ شرودینگر مانند قانون دوم نیوتون عمل می نماید، همانگونه که در فیزیک کلاسیک قانون نیوتون، موقعیت ذره را برای تمام زمان ها مشخص می کند، با داشتن شرایط اولیۀ مناسب می توان معادلۀ موج را در کوآنتوم به وسیله معادلۀ شرودینگر برای همه زمان ها محاسبه نمود. همچنین، روش های گوناگونی، برای حل معادلۀ شرودینگر ارائه شده است که از جمله آنها می توان به روش فاکتوریزاسیون، روش نیکی فرو-یووارو، روش ابرتقارن، روش المان محدود اشاره نمود.
همچنین، گروهی از محققان به حل تابع شرودینگر به عنوان یک تابع کاملاً ریاضی، در دو بخش، روشهای عددی وروشهای تحلیلی پرداخته اند. در روش حل تحلیلی تابع شرودینگر می توان به کار صدیقی و گنجی اشاره نمود که با استفاده از تکنیک هموتوپی در توپولوژی، توابع گوناگون شرودینگر یک بعدی وابسته به زمان را به دست آورده اند. به علاوه، ویتانوف و دیمیتروا از روش اصلاح شده ساده ترین معادله برای تحلیل معادلات غیرخطی شرودینگر استفاده نمودند. علاوه براین، روش بدون المان پتروف – گالرکین محلی برای حل عددی معادلۀ شرودینگر وابسته به زمان سه بعدی و دو بعدی، روش بی اسپلاین،روش توابع پایۀ شعاعی می باشد. علاوه براین، سیادوی معادلۀ شرودینگر غیرخطی را با استفاده از یک تابع تبدیل به معادلۀ شرودینگرخطی تبدیل کرده و حل دقیق آن را به دست آورده است. معادلۀ شرودینگر غیرخطی مکعبی در بسیاری از مباحث فیزیکی نمایان می گردد؛ برای نمونه در علم اپتیک، این معادله انتشار بالای یک پرتوی لیزر در یک وسیله را وقتی که از توزیع وارون امواج رادیویی چشم پوشی شده باشد، کنترل می کند. تحقیقات حاکی ازاین می باشد که همه معادله هایی که دارای حل سالیتونی هستند، همچون معادله های شرودینگر غیرخطی، گوردن سینوسی و شفافیت خودالقا، از حدود ویسکوزیته گوناگونی ناشی می شوند.
توجه داشته باشیم که با حل معادله ی شرودینگر، ویژه توابع و ویژه مقادیر انرژی سیستم در حضور برهمکنش اسپین- مدارومیدانهای خارجی را می توان محاسبه کرده و با روشهای عددی ویژه مقادیر و ویژه توابع جدید سیستم محاسبه می شود. در سیستمهای کوانتومی یک بعدی ویژه مقادیر را با استفاده از روشهای جبری و ویژه توابع حالت های مقیّد را با استفاده از عملگرهای ایجاد شده از جبرِ لی و تأثیر آن بر حالت پایه می توان مشخص نمود. بهلاوه، هرگاه عملگرها بتوانند ویژه توابعِ وابسته به ویژه مقادیر یکسان سیستم ها را با پارامترهای پتانسیلی مختلفی ایجاد کنند، جبر به کار رفته جبرِ پتانسیلی خواهد بود و روش جبری نتایجی را برای خانواده پتانسیلی ارائه خواهد داد، از این رو، این روش را تقارن دینامیکی می گویند. لازم به ذکر است، زمانی حل معادله شرودینگر میتواند یک مسئلۀ جبری باشد که آن مسئله با استفاده از ابزار نظریە ی گروه قابل بررسی باشد.
همچنین، معادالت شرودینگرِ دقیقاً حل پذیر در مکانیک کوانتومی یک موقعیت قطبی را اشغال می کنند تا آنجا که بیشتر آنها به سیستم های فیزیکی مربوط می گردند. نمونۀ جالبِ آن، پتانسیلِ پاشل- تلر است که به عنوان یک میدانِ میانگینِ مؤثّر در سیستم های چندجسمی با برهمکنش ها ظاهر می شود.مطلب قابل توجه این است که، از کاربردهای پتانسیل پاشل- تلر می توان به بررسی مسئلۀ الکترون و حفره از راه این پتانسیل اشاره نمود. پارامترهای فیزیکی کنترل کننده ی نقاط کوانتومی نه تنها از نظر علوم بنیادی بلکه به علت کاربرد بالقوّه ی آن در توسعە ی دستگاه های الکترونیکی نیمه رسانا جذّاب می باشند.