مقدمه ای بر الگوریتم های تکاملی

الگوریتم های تکاملی چیست؟

الگوریتم های تکاملی یک برنامه ی کامپیوتری مبتنی بر هوش مصنوعی تکاملی است که با استفاده از فرآیندهایی که رفتارهای موجودات زنده را تقلید می‌کنند، مسایل را حل می‌کند. به این ترتیب، از مکانیسم هایی استفاده می کند که معمولاً با تکامل بیولوژیکی مرتبط هستند، مانند تولید مثل، جهش و جایگزینی ترکیب.
به طور کلی الگوریتم‌های تکاملی یک رویکرد مبتنی بر اکتشافات و برای حل مسائلی هستند که به راحتی در زمان چند جمله‌ای قابل حل نیستند، مانند مسائل کلاسیک سخت از درجه NP-Hard، و هر چیز دیگری که پردازش کامل آنها بسیار طولانی است وزمانی که به تنهایی مورد استفاده قرار می گیرند، معمولاً برای مسایل ترکیبی استفاده می شوند. با این حال، الگوریتم‌های تکاملی ژنتیک اغلب همراه با روش‌های دیگر مورد استفاده قرار می‌گیرند تا عنوان یک راه حل سریع برای یافتن یک مکان شروع بهینه برای الگوریتم دیگرعمل می‌کنند.
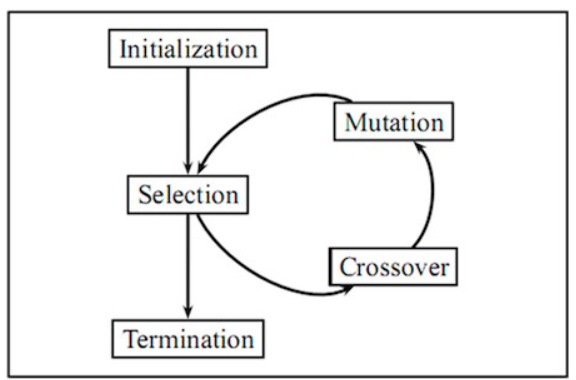
اگر شما با فرآیند انتخاب طبیعی و تصادفی آشنا باشید،به عنوان مثال در الگوریتم ژنتیک شناخت یک الگوریتم تکاملی (که بیشتر به عنوان EA شناخته می شود) بسیار ساده است. یک EA یا همان الگوریتم تکاملی شامل چهار مرحله کلی است: مقداردهی اولیه، انتخاب، عملگرهای ژنتیکی و خاتمه. این مراحل هر کدام تقریباً با جنبه خاصی از انتخاب طبیعی مطابقت دارند و راه‌های آسانی برای مدلسازی و پیاده‌سازی‌های این دسته الگوریتم ارائه می‌دهند. به بیان ساده، در یک EA، اعضای مناسب‌تر یا همان انتخاب های مناسب زنده می‌مانند و تکثیر می‌شوند، در حالی که اعضای نامناسب از بین می‌روند و مانند انتخاب طبیعی، به مخزن ژنی نسل‌های بعدی (انتخاب های بعدی) کمک نمی‌کنند.

 مقداردهی اولیه (Initialization)

در اینجا، به طور کلی مسیله را اینگونه تعریف می کنیم:
برای شروع الگوریتم خود، ابتدا باید یک جمعیت اولیه از راه حل ها ایجاد کنیم. جمعیت شامل تعداد دلخواه از راه حل های ممکن برای مسیله است که اغلب اعضا یا جمعیت نامیده می شوند. اغلب به‌طور تصادفی (در چارچوب محدودیت‌های مسئله) ایجاد می‌شود، واصولا حول محور چیزی است که تصور می‌شود ایده‌آل است. مهم است که جمعیت طیف وسیعی از راه حل ها را در بر گیرد، زیرا اساساً نشان دهنده یک مخزن ژنی یا مجموعه ای از ژن ها است. بنابراین، اگر بخواهیم بسیاری از احتمالات مختلف را در طول الگوریتم کاوش کنیم، باید ژن‌های مختلف را در اختیار داشته باشیم.

انتخاب (Selection)

پس از ایجاد یک جمعیت، اعضای جمعیت اکنون باید بر اساس یک تابع تناسب برازش ارزیابی شوند. تابع تناسب تابعی است که ویژگی های یک عضو را می گیرد و یک نمایش عددی از میزان قابل اجرا بودن یک راه حل را به بیرون ارائه می دهد. ایجاد تابع برازش اغلب می تواند بسیار دشوار باشد، و یافتن یک تابع خوب که به طور دقیق داده ها را نشان می دهد مهم است. این بسیار مشکل خاص است. حال، تابع تناسب برازش همه ی اعضا را محاسبه کرده و بخشی از اعضای دارای امتیاز برتر را انتخاب می کنیم.

توابع اهداف چندگانه

EA ها (الگوریتم های تکاملی )همچنین می توانند برای استفاده از چندین عملکرد تابع برازش گسترش یابند. این روند تا حدودی پیچیده می باشد زیرا به جای اینکه بتوانیم یک نقطه بهینه را شناسایی کنیم، یا در هنگام استفاده از چندین تابع برازش با مجموعه ای از نقاط بهینه مواجه می شویم. مجموعه راه حل های بهینه مرز پارتو نامیده می شود و شامل عناصری است که به همان اندازه بهینه هستند به این معنا که هیچ راه حلی بر هیچ راه حل دیگری در الگوریتم غالب نیست. سپس از یک الگوریتم تصمیم‌گیرنده استفاده می کنیم تا مجموعه را به یک راه‌حل یکتا، بر اساس تیوری مسئله یا برخی معیارهای دیگر محدود کند.

عملگرهای ژنتیکی

این مرحله واقعاً شامل دو مرحله فرعی است: ترکیب و جهش. پس از انتخاب اعضای برتر (با فرض مثال 2 نفر برتر، اما این تعداد می تواند متغیر باشد)،حال از این اعضا برای ایجاد نسل بعدی در الگوریتم استفاده می کنیم و با استفاده از ویژگی‌های والدین منتخب، فرزندان جدیدی خلق می‌شوند که ترکیبی از ویژگی‌های والدین هستند. انجام این کار بسته به نوع داده‌ها اغلب ممکن است دشوار باشد، اما معمولاً در مسائل ترکیبی، می‌توان ترکیب‌ها را با هم ترکیب کرد و جایگزین کرد و ترکیب‌های معتبر خروجی را از این ورودی‌ها به دست آورد. اکنون باید موارد ژنتیکی جدیدی را وارد نسل کنیم.
اگر این مرحله حیاتی را انجام ندهیم، خیلی سریع در مرحله های بعدی اشتباه می کنیم و به نتایج مطلوب نمی رسیم. این مرحله یک جهش است وما این کار را به سادگی با تغییر دادن بخش کوچکی از فرزندان (همان انتخاب های مناسب) به گونه‌ای انجام می‌دهیم که دیگر زیرمجموعه‌ها از ژن‌های والدین را کاملاً منعکس نکند. جهش معمولاً به صورت احتمالی و تصادفی اتفاق می‌افتد، به این صورت که اگر شانس دریافت جهش و همچنین شدت جهش توسط یک توزیع احتمالی کنترل شود.

مرحله ی نهایی (Termination)

در نهایت بعد از گذر از مراحل انتخاب. جهش و ترکیب، الگوریتم باید به پایان برسد. معمولاً دو مورد وجود دارد: یا الگوریتم به حداکثر زمان اجرا رسیده است یا الگوریتم به آستانه ی عملکرد خود رسیده است. در این مرحله، یک راه حل نهایی انتخاب شده و برگردانده می شود و الگوریتم درست اجرا می شود.
حال می خواهیم بدانیم مزایای کسب و کار الگوریتم های تکاملی چیست؟

مزایای کسب و کار متعدد با الگوریتم های تکاملی مرتبط است، از جمله:

افزایش انعطاف پذیری مفاهیم الگوریتم های تکاملی را می توان برای حل پیچیده ترین مشکلاتی که انسان ها با آن مواجه هستند و به اهداف مورد نظر دست یافتن، اصلاح و تطبیق داد.
بهینه سازی بهتر یا “جمعیت” گسترده همه ی راه حل های ممکن را در نظر می گیرد. این بدان معناست که الگوریتم به یک راه حل خاص محدود نمی شود.
راه حل های نامحدود برخلاف روش‌های کلاسیک که بهترین راه‌حل را ارائه می‌کنند و تلاش می‌کنند تا بهترین راه‌حل را حفظ کنند، اما الگوریتم‌های تکاملی شامل راه‌حل‌های بالقوه متعدد برای یک مسئله هستند و می‌توانند راه حل هایی را ارائه دهند.

دو مسئله مهم برای ما اینجا وجود دارد که باید قبل از استفاده از یک الگوریتم تکاملی برای یک مسیله خاص رعایت شود

در مرحله ی اول، ما به مسیری سوق داده می شویم که برای رمزگذاری راه حل هایی برای انتخاب در مسیله نیاز داریم. ساده‌ترین رمزگذاری که توسط بسیاری از الگوریتم‌های ژنتیک استفاده می‌شود، یک رشته بیت است. هر انتخاب ما به سادگی دنباله ای از صفر و یک است.

این رمزگذاری، جهش وترکیب یا متقاطع را بسیار ساده می کند، اما این بدان معنا نیست که نمی توانیم از نمایش های پیچیده تری استفاده کنیم. در واقع، چندین نمونه ی پیشرفته تر از انتخاب ها را در مرحله های بعدی الگوریتم خواهیم دید. تا زمانی که بتوانیم طرح یا مدلی دقیق برای تکامل انتخاب ها طراحی کنیم، واقعاً هیچ محدودیتی برای انواعی که می توانیم استفاده کنیم وجود ندارد. برنامه نویسی ژنتیکی (GP) مثال خوبی برای این موضوع است. GP برنامه های کامپیوتری را که به صورت پیمایش درخت های نحوی نمایش داده می شوند، تکامل می دهد.
گام دوم برای به کارگیری الگوریتم های تکاملی این است که باید راهی برای ارزیابی راه حل های جزئی برای مسئله وجود داشته باشد . تابع برازش یا ارزیابی درست یا غلط راه حل ها کافی نیست، ارزیابی تابع برازش باید نشان دهد که راه حل انتخابی چقدر درست است یا اگر لیوان شما نیمه خالی است، چقدر خالی است. بنابراین تابعی که 0 یا 1 را برمی گرداند بی فایده است. تابعی که امتیازی را در مقیاس 1 تا 100 برمی گرداند بهترو بهینه تر است. ما به سایه‌های خاکستری نیاز داریم، نه فقط سیاه و سفید، چون این روشی است که الگوریتم های تکاملی تصادفی را برای یافتن راه‌حل‌های بهتر هدایت می‌کند.