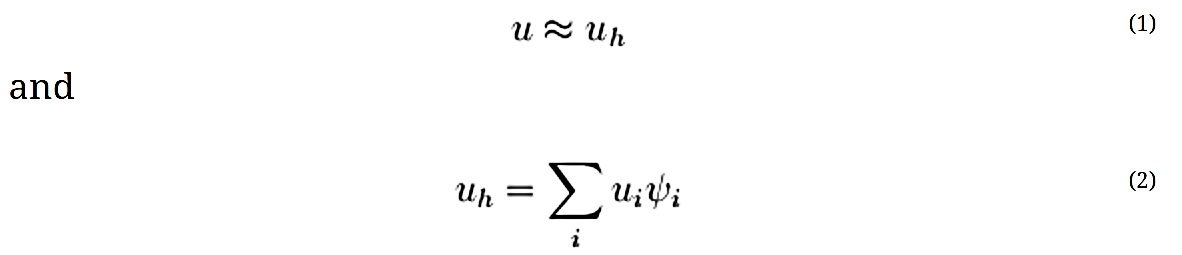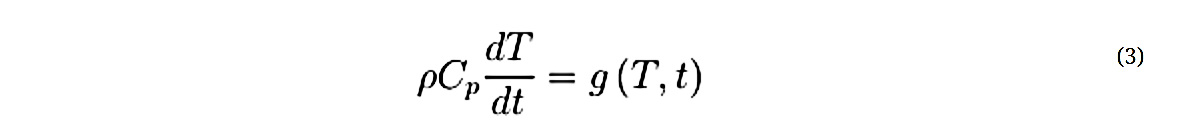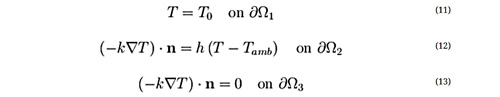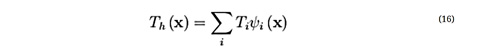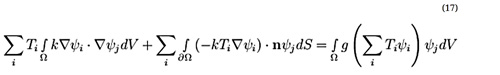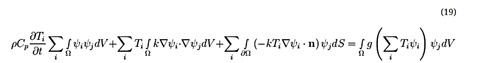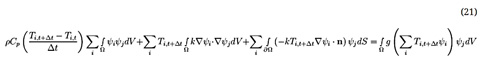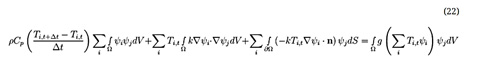روش المان محدود چیست؟

• مقدمه ای بر روش اجزای (المان) محدود

شرح قوانین فیزیک برای مسایل وابسته به فضا و زمان معمولاً براساس معادلات دیفرانسیل جزئی (PDE) بیان می‌شود. برای اکثر قریب به اتفاق هندسه‌ها و مسائل، این PDE‌ها با روش‌های تحلیلی حل نمی‌شوند. درعوض، می‌توان تقریب معادلات را بر اساس انواع روش های مختلف گسسته‌سازی کرد. این روش‌های گسسته‌سازی،  PDE‌ها را با معادلات مدل های عددی تقریب می‌زنند، که با استفاده از روش‌های عددی می‌توان آن‌ها را حل کرد. راه حل معادلات مدل های عددی، به نوبه خود، تقریبی از راه حل واقعی PDE ‌ها است. برای محاسبه چنین تقریب‌هایی از روش المان محدود (FEM) استفاده می‌شود.

به عنوان مثال یک تابع u را در نظر بگیرید که ممکن است متغیر وابسته در PDE باشد (یعنی دما، پتانسیل الکتریکی، فشار و غیره) تابع u را می‌توان با یک تابع uh با استفاده از ترکیبات خطی توابع پایه مطابق زیر تقریب زد:

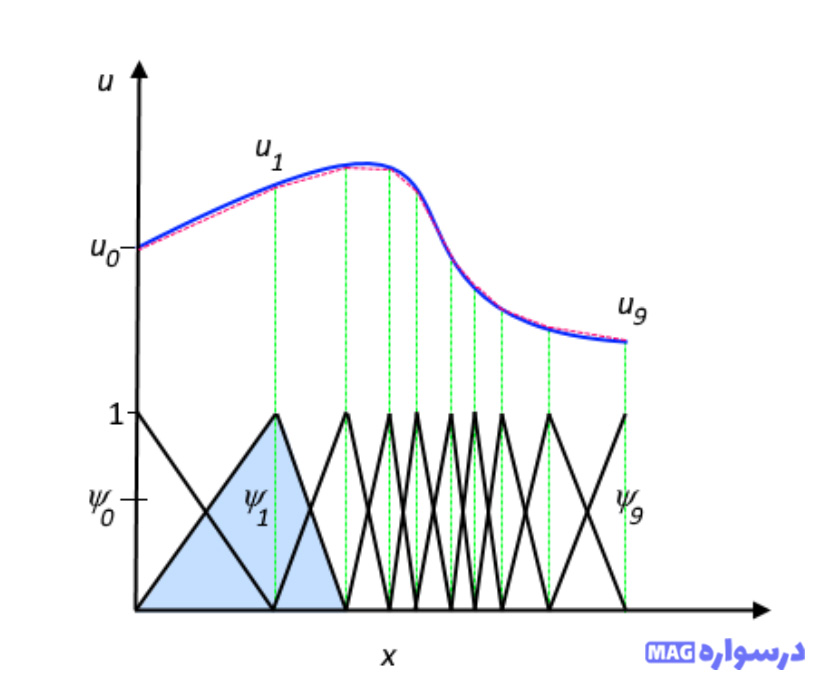
در اینجا، ψi توابع پایه را نشان می‌دهد و ui ضرایب توابع را نشان می‌دهد که u را با uh تقریب می‌کند. شکل زیر این اصل را برای یک مسئله یک بعدی نشان می‌دهد. به عنوان مثال، u می‌تواند دما را در امتداد طول (x) یک میله که به طور غیر یکنواخت گرم می‌شود، نشان دهد. در اینجا، توابع پایه خطی در گره های مربوطه 1 و در گره های دیگر مقدار 0 دارند. در این حالت ، هفت المان در امتداد بخشی از محور x وجود دارد ، جایی که تابع u تعریف شده است (به عنوان مثال ، طول میله).

* تابع u (خط آبی توپر) که با uh (خط چین قرمز) تقریب زده شده است یک ترکیب خطی از توابع پایه خطی است (ψi با خطوط سیاه توپر نشان داده می شود). ضرایب با u0 تا u7 نشان داده شده اند.

هر دوی این توابع نشان می‌دهند که توابع پایه خطی انتخاب شده شامل پوشش بسیار محدود (بدون صفر فقط در یک بازه کم) و همپوشانی در امتداد محور x هستند. بسته به مسئله موجود، ممکن است توابع دیگری به جای توابع خطی انتخاب شوند. یکی دیگر از مزایای روش اجزای محدود این است که تئوری آن به خوبی توسعه یافته شده است. دلیل این امر ارتباط نزدیک بین فرمول بندی عددی و شکل ضعیف فرمول بندی (weak formulation) مسائل PDE است (بخش زیر را ببینید). به عنوان مثال، هنگامی که معادلات مدل عددی در رایانه حل می‌شود، این تئوری تخمین‌های مفیدی از خطا یا مرز‌های خطا را ارائه می‌دهد.

با نگاهی به تاریخچه FEM ، سودمندی این روش اولین بار در آغاز دهه 1940 توسط ریچارد کورانت ، ریاضیدان آلمانی-آمریکایی شناخته شد. در حالی که Courant کاربرد آن را در مورد طیف وسیعی از مسائل تشخیص داد ، چندین دهه طول کشید تا این رویکرد به طور کلی در زمینه های خارج از مکانیک سازه اعمال شود و به همان چیزی تبدیل شود که امروز است.

*گسسته سازی، تنش ها و تغییر شکل اجزای چرخ در یک تحلیل جامداتی

• معادلات جبری، معادلات دیفرانسیل معمولی، معادلات دیفرانسیل جزئی و قوانین فیزیک

قوانین فیزیک اغلب به زبان ریاضیات بیان می شود. به عنوان مثال ، قوانین بقا از قبیل قانون بقای انرژی ، بقای جرم و بقای اندازه حرکت (مومنتوم) همگی می توانند به صورت معادلات دیفرانسیل جزئی (PDE) بیان شوند. از روابط سازنده ای ممکن است برای بیان این قوانین بر حسب متغیرهایی مانند دما ، چگالی ، سرعت ، پتانسیل الکتریکی و سایر متغیرهای وابسته استفاده شود. از روابط مکمل ممکن است برای بیان این قوانین بر حسب متغیرهایی مانند دما ، چگالی ، سرعت ، پتانسیل الکتریکی و سایر متغیرهای وابسته استفاده شود.

معادلات دیفرانسیل شامل عباراتی است که یک تغییر کوچک در یک متغیر وابسته را با توجه به تغییر در یک متغیر مستقل  (x، y، z، t ) تعیین می‌کند. از این تغییر کوچک به عنوان مشتق متغیر وابسته با توجه به متغیر مستقل نیز یاد می‌شود. فرض کنید یک جامد با دمای متغیر با زمان وجود دارد اما تغییرات ناچیزی در فضا دارد. در این حالت، معادله بقای انرژی داخلی (حرارتی) ممکن است به یک معادله ب تغییر دما، نسبت تغییر زمان بسیار کوچک، به دلیل منبع گرمایی g منجر شود:

در اینجا، چگالی و Cp ظرفیت گرمایی را نشان می‌دهد. دما، T، متغیر وابسته است و زمان، t، متغیر مستقل است. این تابع g ممکن است یک منبع حرارتی را توصیف کند که با دما و زمان تغییر می کند. معادله (۳) بیان می‌کند که اگر تغییر دمایی نسبت به زمان ایجاد شود، باید این تغییر نسبت به منبع حرارتی متعادل شود یا در اثر آن ایجاد شود. این معادله یک معادله دیفرانسیل است که با توجه به مشتقات یک متغیر مستقل (t) بیان می‌شود. چنین معادلات دیفرانسیل به عنوان معادلات دیفرانسیل معمولی (ODE) شناخته می‌شوند.

در برخی شرایط، دانستن دما در یک زمان t0 که شرایط اولیه نامیده می‌شود، اجازه می‌دهد تا یک راه حل تحلیلی از معادله 3 به صورت زیر قابل بیان باشد:

بنابراین درجه حرارت در جامد از طریق یک معادله جبری (۴) بیان می‌شود، جایی که قرار دادن مقدار زمان، t1، مقدار دمایT1 را در آن زمان برمی گرداند. اغلب اوقات، در زمان و مکان تغییرات وجود دارد. برای مثال، درجه حرارت در جامدات در موقعیت‌های نزدیکتر به یک منبع حرارتی ممکن است کمی بالاتر از جا‌های دیگر باشد. چنین تغییراتی باعث ایجاد شار حرارتی بین قسمت‌های مختلف درون جامد می‌شود. در چنین مواردی، بقای انرژی می‌تواند منجر به یک معادله انتقال گرما شود که تغییرات هر دو زمان و متغیر‌های مکانی (x) را بیان می‌کند، مانند:

مانند قبل ، T متغیر وابسته است ، در حالی که x (x = (x, y, z)) و t متغیرهای مستقل هستند. بردار شار گرما در ماده جامد با q = (q_x, q_y, q_z)، ، نشان داده می شود در حالی که دیورژانس q تغییر در شار گرما را در طول مختصات مکانی توصیف می کند. برای یک سیستم مختصات دکارتی ، دیورژانس q به این صورت تعریف می شود:

شار گرما در یک جامد را می‌توان با رابطه شار گرما توسط هدایت توصیف کرد که به عنوان قانون فوریه توصیف می‌شود:

در معادله فوق، k‌ رسانایی گرمایی را نشان می‌دهد. معادله (۷) بیان می‌کند که شار گرما متناسب با گرادیان دما و ‌رسانایی گرمایی به عنوان ثابت تناسب است. معادل (۷) در (۵) معادله دیفرانسیل زیر را ارائه می‌دهد:

در اینجا مشتقات بر حسب  t، x، y و z بیان می‌شوند. هنگامی که یک معادله دیفرانسیل با توجه به مشتقات بیش از یک متغیر مستقل بیان می‌شود، از آن به عنوان معادله دیفرانسیل جزئی (PDE) یاد می‌شود، زیرا هر مشتق ممکن است نشان دهنده یک تغییر در یک جهت از چندین جهت ممکن باشد. علاوه بر این توجه داشته باشید که مشتقات موجود در ODE با استفاده از d بیان می‌شوند، در حالی که مشتقات جزئی با استفاده از ∂ بیان می‌شوند.

علاوه بر معادله (۸)، دما در یک زمان t0 و دما یا شار گرما در برخی از موقعیت‌های x0 نیز می‌تواند شناخته شود. چنین دانشی را می‌توان در مورد شرایط اولیه و مرزی را میتوان برای حل معادله  8 استفاده کرد. در بسیاری از شرایط، PDE‌ها را نمی‌توان با روش‌های تحلیلی حل کرد تا مقدار متغیر‌های وابسته را در زمان‌ها و موقعیت‌های مختلف محاسبه کرد. به عنوان مثال به دست آوردن یک عبارت تحلیلی از جمله:

به جای حل PDE به صورت تحلیلی، یک گزینه جایگزین جستجوی راه حل‌های عددی تقریبی برای حل معادلات مدل عددی است. روش المان محدود دقیقاً همین نوع روش است – یک روش عددی برای حل PDE‌ها. مشابه بقای انرژی حرارتی که در بالا به آن اشاره شد، می‌توان معادلاتی را برای بقای مومنتوم جرم استخراج کرد که اساس حرکت سیال را تشکیل می‌دهند. بعلاوه، معادلات میدان‌های الکترومغناطیسی و شار‌ها را می‌توان برای مسائل وابسته به فضا و زمان بدست آورد و سیستم‌های PDE را تشکیل داد. در ادامه این بحث، بیایید ببینیم که چگونه فرمولاسیون به اصطلاح ضعیف می‌تواند از PDE استخراج شود.

• روش اجزای محدود از فرمول بندی ضعیف: توابع پایه و توابع آزمون

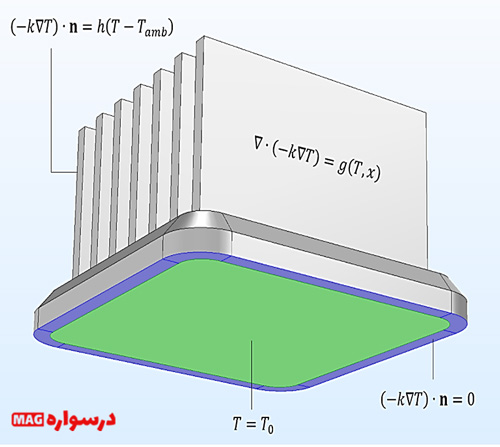
فرض کنید که توزیع دما در یک مخزن گرمایی (heat sink) در حال مطالعه است که توسط معادله 8 در شراط پایا به این معنی که مشتق زمانی میدان دما در معادله صفر است داده شده است. معادله میدان برای دامنه مدل، Ω  به شرح زیر است:

علاوه بر این، فرض کنید که درجه حرارت در امتداد یک مرز (∂Ω₁) مشخص باشد، علاوه بر این برای شار گرما عمود به برخی از مرز‌های دیگر (∂Ω₂) است. در مرز‌های باقیمانده، شار گرما در جهت خارج صفر است (∂Ω₃). پس شرایط مرزی در این مرز‌ها به شرح زیر است:

که در آن h ضریب انتقال حرارت و T_amb دمای محیط را نشان می‌دهد. بردار عمود واحد خارج به سطح مرز با n نشان داده می‌شود. معادلات (۱۰) تا (۱۳) مدل ریاضی برای سینک حرارتی را توصیف می‌کند، همانطور که در زیر نشان داده شده است.

* معادله میدان و شرایط مرزی برای یک مدل ریاضی از یک مخزن گرمایی

مرحله بعدی ضرب هر دو طرف معادله (10) در یک تابع آزمون φ و انتگرال گیری روی دامنه Ω است.

فرض می‌شود که تابع آزمون φ و حل T متعلق به فضا‌های هیلبرت باشد. فضای هیلبرت یک فضای تابعی بی‌نهایت بعدی با توابع خواص مشخصی است. می‌توان آن را به عنوان مجموعه‌ای از توابع با خصوصیات خوب معلومی تصور کرد، به طوری که می‌توان این توابع را به راحتی همانند بردار‌های معمولی در یک فضای بردار دستکاری کرد. به عنوان مثال، شما می‌توانید ترکیبات خطی توابع در این مجموعه را تشکیل دهید (توابع دارای یک طول کاملاً مشخص هستند که از آن به عنوان عمود یاد می‌شود) و می‌توانید زاویه بین توابع را اندازه‌گیری کنید، دقیقاً مانند بردار‌های اقلیدسی.

در واقع ، پس از استفاده از روش اجزای محدود روی این توابع ، آنها به سادگی به بردارهای معمولی تبدیل می شوند. روش المان محدود روشی سیستماتیک برای تبدیل توابع در یک فضای تابعی بی نهایت بعدی ابتدا به توابع در یک فضای تابعی اولیه محدود و سپس در نهایت بردارهای معمولی (در یک فضای برداری) است که با روش های عددی قابل جمع شدن هستند.

فرمول ضعیف، یا فرمول متغیر، از معادله (۱۰) با الزام به رعایت این برابری برای همه توابع تست در فضای هیلبرت بدست می‌آید. این فرم ضعیف نامیده می‌شود زیرا ملزومات (۱۰) را آرام (Relax) می‌کند، جایی که تمام اجزای PDE باید در همه نقاط به خوبی تعریف شود. روابط در (۱۴) و (۱۵) در عوض فقط در فضای انتگرال به تساوی نیاز دارند. به عنوان مثال، ناپیوستگی اولین مشتق برای حل کاملاً توسط فرمولاسیون ضعیف مجاز است زیرا مانع انتگرال گیری نمی‌شود. با این حال، توزیعی برای مشتق دوم معرفی می‌کند که در فضای معمولی تابع نیست. بدین ترتیب، الزام (۱۰) در مرحله ناپیوستگی نیست.

یک توزیع می‌تواند گاهی اوقات انتگرال گرفته شود و (۱۴) به خوبی تعریف شود. می‌توان نشان داد که فرمول ضعیف، همراه با شرایط مرزی (۱۱) تا (۱۳)، مستقیماً با حل از فرمول نقطه‌ای ارتباط دارد. و، برای مواردی که راه حل به اندازه کافی قابل مشتق گیری است (به عنوان مثال، هنگامی که مشتقات دوم به خوبی تعریف شده اند)، این راه حل‌ها یکسان هستند. معادلات در موازنه هستند، زیرا بدست آوردن (۱۵) از (۱۰) به اولین اتحاد گرین (Green’s first identity) متکی است، که فقط در صورت داشتن مشتقات ثانویه T  برقرار است.

این اولین مرحله در فرمول‌بندی المان محدود است. با فرمول‌بندی ضعیف، می‌توان با گسسته سازی معادلات ریاضی معادلات عددی را بدست آورد. روش گالرکین – یکی از بسیاری از فرمول‌بندی‌های ممکن برای روش اجزای محدود است که می‌تواند از آن برای گسسته‌سازی استفاده کرد. نخست، گسسته‌سازی به معنای جستجوی یک راه حل تقریبی برای معادله (۱۵) در یک فضای کوچک با ابعاد محدود متناسب با فضای هیلبرت H به گونه‌ای است که در آن .T=T_h  این بدان معناست که حل تقریبی به صورت ترکیبی خطی از مجموعه توابع پایه ψi که متعلق به فضای زیر است بیان می‌شود:

نسخه گسسته‌سازی شده معادله ۱۵ برای هر تابع تست به صورت زیر بدست می‌آید:

در اینجا نامعلوم ها ضرایب Ti در تقریب تابع T (x) است. معادله (۱۷) سپس یک سیستم معادلات از همان بعد فضای تابع  با ابعاد محدود تشکیل می‌دهد. اگر n تعداد توابع آزمون ψj استفاده شود به طوری که j از ۱ به n برسد، یک سیستم تعداد n تعداد معادلات مطابق با (۱۷) بدست می‌آید. از معادله (۱۶)، همچنین n ضریب نامعلوم (Ti) وجود دارد.

• مسائل وابسته به زمان

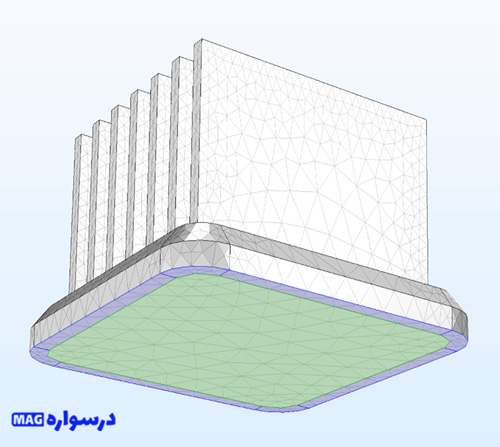
*گسسته سازی المان محدود از مدل سینک حرارتی از شکل قبلی

هنگامی که سیستم گسسته شد و شرایط مرزی اعمال شد، یک سیستم معادلات با توجه به عبارت زیر بدست می‌آید:

که T بردار مجهولات است، T _h = {T₁, .., T_i, …, T_n} و A یک ماتریس nxn است که حاوی ضرایب Ti در هر معادله j در اجزای آن Aji است. سمت راست برداری از بعد ۱ تا n است. A ماتریس سیستم است که غالباً به آن ماتریس سختی (حذف شده) گفته می‌شود و به اولین کاربرد روش اجزای محدود و همچنین استفاده از آن در مکانیک سازه برمی گردد.

اگر تابع منبع (source function) از نظر دما غیر خطی باشد یا ضریب انتقال حرارت به دما بستگی داشته باشد ، سیستم معادله نیز غیر خطی است و بردار b به یک تابع غیر خطی از ضرایب ناشناخته Ti تبدیل می شود.

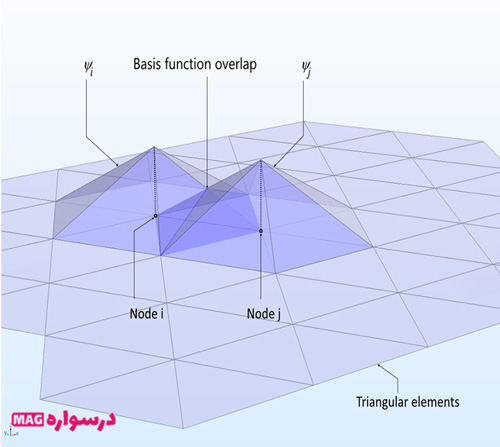
یکی از مزایای روش اجزای محدود توانایی آن در انتخاب توابع آزمون و مبنا است. می توان توابع آزمون و مبنایی را که در یک منطقه هندسی بسیار کوچک پشتیبانی می شوند ، انتخاب کرد. این نشان می دهد که انتگرال ها در معادله. (17) در همه جا صفر است ، مگر در مناطق بسیار محدود که توابع ψj و ψi با هم همپوشانی داشته باشند ، زیرا تمام انتگرال های فوق شامل محصولات توابع یا شیب های توابع i و j هستند. به سختی می توان پشتیبانی از توابع آزمون و مبنای سه بعدی را به تصویر کشید ، اما می توان قیاس دوبعدی را تجسم کرد.

فرض کنید که یک دامنه هندسی ۲ بعدی وجود دارد و توابع خطی x و y انتخاب می‌شوند که هر یک در نقطه i مقدار ۱ دارند، اما در سایر نقاط k  صفر هستند. مرحله بعدی تشخیص دامنه دوبعدی با استفاده از مثلث‌ها و به تصویر کشیدن چگونگی ظاهر شدن دو توابع پایه (توابع آزمون یا شکل) برای دو‌گره همسایه i و j در یک شبکه مثلثی است.

* توابع پایه خطی چادر شکل که در گره مربوطه مقدار 1 و در سایر گره ها صفر دارند. دو تابع پایه که یک المان را به اشتراک می گذارند در تابع مبنا همپوشانی دارند.

دو تابع پایه همسایه دارای دو المان مثلثی مشترک هستند. به همین ترتیب ، همانطور که در بالا نشان داده شده است ، بین دو تابع پایه همپوشانی وجود دارد. بعلاوه ، توجه داشته باشید که اگر i = j باشد ، یک تداخل کامل بین توابع وجود دارد. این مشارکت بین ضرایب بردار ناشناخته T را تشکیل می دهند که با اجزای مورب ماتریس سیستم Ajj مطابقت دارند.

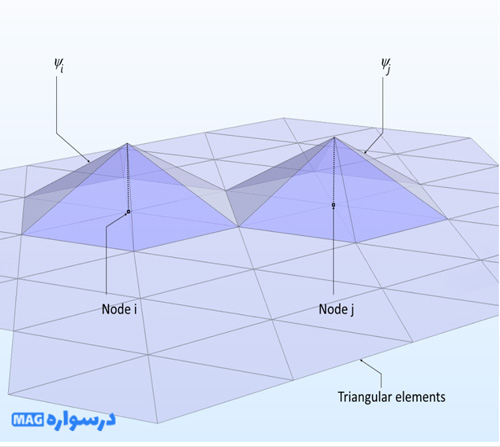
فرض کنید که اکنون دو تابع مبنا کمی فاصله دارند. این توابع المانی را به اشتراک نمی گذارند اما یک راس عنصر مشترک دارند. همانطور که در شکل زیر مشخص است ، آنها با هم تداخل ندارند.

*دو تابع پایه که یک رأس عنصر را به اشتراک می گذارند اما در یک دامنه 2 بعدی همپوشانی ندارند

هنگامی که توابع پایه با هم همپوشانی دارند، انتگرال‌ها در معادله (۱۷) مقدار غیر صفر دارند و مشارکت در ماتریس سیستم غیر صفر است. در صورت عدم همپوشانی، انتگرال‌ها صفر هستند و بنابراین سهم ماتریس سیستم نیز صفر است. این بدان معناست که هر معادله در سیستم معادلات (۱۷) برای‌گره‌های ۱ تا n فقط چند جز غیر صفر از‌گره‌های همسایه که المان مشابهی دارند، بدست می‌آورد. ماتریس سیستم A در معادله  (۱۸) پراکنده می‌شود، فقط با ترم های غیر صفر برای اجزای ماتریسی که با ij: s همپوشانی دارند مطابقت دارد. حل سیستم معادلات جبری، تقریبی از راه حل PDE می‌دهد. هرچه مش متراکم‌تر باشد، حل تقریبی به حل واقعی نزدیکتر می‌شود.

*تقریب المان محدود از میدان دما

تعادل انرژی گرمایی در مخزن گرما را می‌توان برای موارد وابسته به زمان را در ادامه تعریف کرد. فرمول ضعیف گسسته برای هر تابع آزمون ψj  با استفاده از روش Galerkin ، می‌تواند به صورت زیر نوشته شود:

در اینجا، ضرایب Ti توابع وابسته به زمان هستند در حالی که توابع پایه و آزمون فقط به مختصات مکانی بستگی دارند. علاوه بر این، مشتق زمان در حوزه زمان گسسته نمی شوند .یک روش استفاده از FEM برای دامنه زمان  نیز هست، اما این می‌تواند از نظر محاسباتی‌ سنگین باشد. با روش جایگزین، گسسته‌سازی مستقل دامنه زمان اغلب با استفاده از روش خطوط اعمال می‌شود. به عنوان مثال، می‌توان از روش تفاضل محدود استفاده کرد. در ساده‌ترین شکل، این را می‌توان با تقریب دیفرانسیل زیر بیان کرد:

دو تقریب نفاضل محدود بالقوه مسئله در معادله (۱۹) آورده شده است. اولین فرمول زمانی است که ضرایب ناشناخته T_t,i  بر حسب t + Δt بیان می‌شوند:

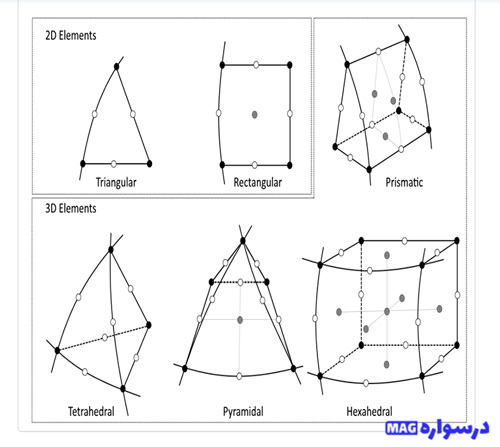
اگر مسئله خطی است، برای هر گام زمانی باید یک سیستم خطی از معادلات حل شود. اگر مسئله غیرخطی است، یک سیستم معادلات غیرخطی مربوط، باید در هر گام زمانی حل شود. از طرح راهپیمایی زمانی (time-marching scheme) به عنوان یک روش ضمنی implicit method یاد می‌شود، زیرا راه حل در t + Δt به طور ضمنی توسط معادله 21 داده می‌شود. فرمول دوم براساس حل  t است:

این فرمول به این معنی است که هرگاه حل (t، Ti) در یک زمان مشخص معلوم شود، معادله (۲۲) صریحاً حل را درt + Δt (Ti, t+Δt) می‌دهد. به عبارت دیگر، برای یک طرح مشخص راهپیمایی زمانی، نیازی به حل یک سیستم معادله در هر مرحله نیست. اشکال در مورد طرح‌های مشخص راهپیمایی زمانی این است که با محدودیت گام به گام پایداری همراه هستند. برای مسائل گرما، مانند مورد گفته شده در اینجا، یک روش صریح به مراحل بسیار کمی نیاز دارد. طرح‌های ضمنی امکان گام‌های بزرگتر زمانی را فراهم می‌کند و هزینه معادلاتی مانند (۲۲) را که باید در هر مرحله زمانی حل شوند کاهش می‌دهد.

در عمل، الگوریتم‌های مدرن گام‌بندی زمانی بسته به مسئله به طور خودکار بین گام‌های صریح و ضمنی جابجا می‌شوند. بعلاوه، معادله دیفرانسیلی (۲۰) با یک جمله چند جمله‌ای جایگزین می‌شود که بسته به مسئله و تکامل حل در طول زمان، ممکن است درجه و طول گام متفاوتی داشته باشد. یک طرح مدرن راهپیمایی زمانی کنترل خودکار ترتیب چند جمله‌ای و طول گام برای تکامل زمان حل عددی را دارد.

در مورد متداول‌ترین روش‌هایی که استفاده می‌شود، در اینجا چند مثال آورده شده است:

روش فرمول دیفرانسیل گیری رو به عقب (BDF)
روش آلفای تعمیم یافته
روش‌های مختلف Runge-Kutta

• انواع المان

همانطور که در بالا ذکر شد، روش Galerkin از همان توابع برای توابع مبنا و توابع آزمون استفاده می‌کند. با این حال، حتی برای این روش، روش‌های زیادی (در تئوری بی‌نهایت زیاد) برای تعیین توابع اساسی (به عنوان مثال، عناصر موجود در فرمول‌بندی المان محدود Galerkin ) وجود دارد. بیایید برخی از رایج‌ترین المان ها را مرور کنیم.

برای توابع خطی در دوبعد و سه بعد، متداول‌ترین المان ها در شکل زیر نشان داده شده است. توابع پایه خطی، همانطور که در یک مش مثلثی شکل تعریف شده و عناصر خطی مثلثی را تشکیل می‌دهد، در این شکل و این شکل بالا نشان داده شده است. توابع مبنا به صورت تابع موقعیت‌گره‌ها در سه بعد بیان می‌شوند .

در دوبعد، المان مستطیلی شکل اغلب در تحلیل مکانیک سازه اعمال می‌شوند. از این نوع المان ها همچنین می‌توان برای شبکه بندی لایه مرزی در CFD و مدل‌سازی انتقال حرارت استفاده کرد. معادل سه بعدی آن‌ها به عناصر شش ضلعی معروف است، و معمولاً در مکانیک سازه و شبکه بندی لایه مرزی استفاده می‌شود. در انتقال از عناصر لایه مرزی شش وجهی به عناصر چهار وجهی، عناصر هرمی معمولاً در بالای عناصر لایه مرزی قرار می‌گیرند.

* محل قرارگیری خطوط و نقاط در المان های خطی

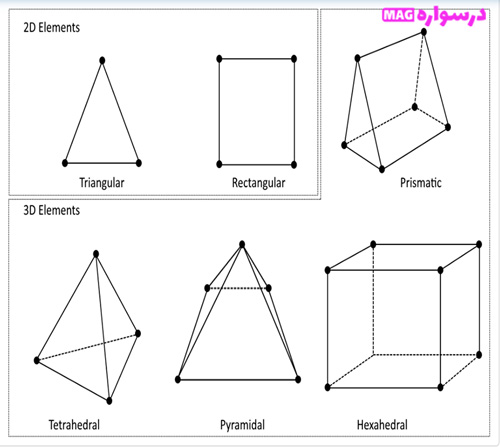
المان های مرتبه دوم مربوطه (المان های درجه دوم) در شکل زیر نشان داده شده است. در اینجا، لبه‌ها و سطوح در مرز دامنه غالباً خمیده هستند، در حالی که لبه‌ها و سطوح رو به قسمت داخلی دامنه، خطوط یا سطوح مسطح هستند. البته توجه داشته باشید که این گزینه وجود دارد که تمام لبه‌ها و سطوح را به صورت خمیده تعریف کنید. المان های لاگرانژی و غیرمعمول متداول‌ترین نوع المان ها در دوبعد و سه بعد هستند. المان های لاگرانژی از همه‌گره‌های زیر (سیاه، سفید و خاکستری) استفاده می‌کنند، در حالی که عناصر غیرمعمول ‌گره‌های خاکستری را حذف می‌کنند.

*المان های مرتبه دوم

هنگام بحث درباره FEM، یک عنصر مهم که باید در نظر گرفت تخمین خطا است. این به این دلیل است که وقتی حد تورولانس خطای تخمینی بدست می‌آید، همگرایی رخ می‌دهد. توجه داشته باشید که بحث در اینجا بیشتر جنبه عمومی دارد تا خاص FEM.

روش المان محدود یک حل تقریبی برای معادلات مدل ریاضی می‌دهد. اختلاف بین حل معادلات عددی و حل دقیق معادلات مدل ریاضی این خطاست: e = u – uh

در بسیاری از موارد، خطا را می‌توان قبل از حل معادلات عددی تخمین زد (یعنی برآورد خطا). برآورد پیشینی غالباً صرفاً برای پیش بینی مرتبه همگرایی روش المان محدود استفاده می‌شود. به عنوان مثال، اگر مسئله به خوبی تعریف شود و روش عددی همگرا شود، نرم خطا با اندازه المان معمولی h با توجه به O (h^α)، جایی که α مرتبه همگرایی را نشان می‌دهد، کاهش می‌یابد. این به سادگی نشان می‌دهد که با متراکم شدن مش، با چه سرعتی نرم خطا کاهش می‌یابد.

یک برآورد را فقط برای مسائل ساده می‌توان یافت. علاوه بر این، تخمین‌ها اغلب حاوی ثابت‌های مختلف نامعلومی هستند و پیش بینی‌های کمی را غیر ممکن می‌کنند. برای برآورد مرتبه خطا، یک برآورد پسینی با استفاده از راه حل تقریبی، در ترکیب با تقریب‌های دیگر مربوط به مسائل منجر به حدس مرتبه خطا می‌شود.